Phase shift

This is denoted by e. A phase shift arises if we start timing the wave motion at an instant when the amplitude is not zero (see Figure 1).

When t = 0 y = a sin ε

Phase change on reflection

It is important to realise the difference between longitudinal (or compression) waves and transverse waves when they are reflected at a boundary.

With the longitudinal wave there is no phase change on reflection if the reflection takes place at a fixed boundary. The particles carrying the vibration rebound elastically from a solid barrier and a compression is reflected as a compression. However a phase change of π occurs at a free boundary, such as the open end of a tube.

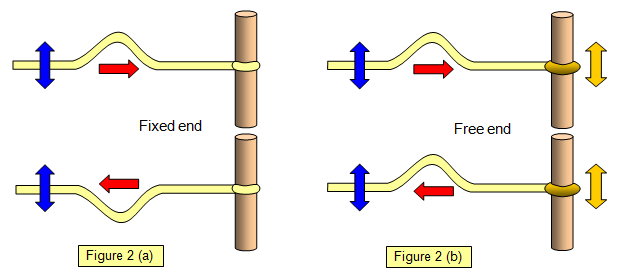
With a transverse wave the phase change also depends on the nature of the boundary. If the boundary is fixed there is a phase change of π (2(a)) but if it is flexible the phase change is less than p, and it is zero at a free boundary (2(b)). You can show this using ropes (see Figure 2).

The phase change of π only occurs on reflection from the fixed end, a crest is reflected back as a trough. This is not the case with the free end nor is it for a water wave hitting the side of a harbour wall - the particles of water are free to move up and down and so no phase change occurs here.

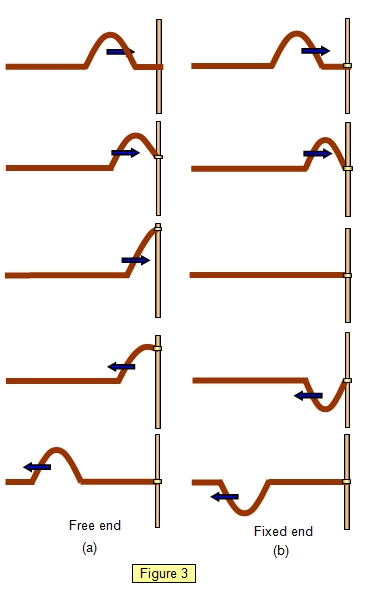
A further more detailed example of free and fixed end reflection is shown in Figures 3(a) and 3(b).

Notice that in the free end pulse the end of the cord moves up the rod as the wave meets it. The movement of the free end stretches the cord and so produces a reflected pulse. The incoming pulse and the reflected pulse reinforce each other and so the reflected pulse has the same phase as the incoming pulse. Notice that the maximum amplitude during reflection is greater than that of the incoming pulse.

In the fixed end pulse the end of the cord exerts an upward force on the rod. By Newton's Third Law the rod therefore exerts a downward force on the cord and so the reflected pulse experiences a change of phase.

Stokes' theorem

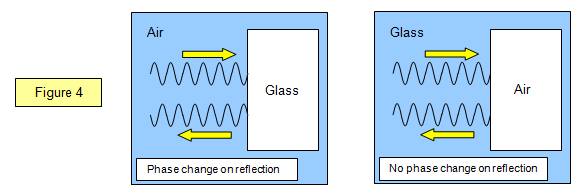
It is possible to introduce a phase difference between two wave trains without an actual path difference, using reflection. If a wave reflects from an optically more dense medium than the one in which it was travelling (e.g when going from air to glass) then a phase change of π is produced, corresponding to an effective path difference of half a wavelength. In Figure 4 two examples are shown, one where light passes from a less dense to a more dense material and the other where the reverse is true.

(Note: only the reflected waves are shown)